Проверка устойчивости движения к поверхности переключения
Необходимо обеспечить устойчивость движения относительно поверхности переключения. Для проверки этого условия воспользуемся вторым методом Ляпунова. Выберем функцию Ляпунова – ![]() такую, чтобы
такую, чтобы ![]() . Этому условию удовлетворяет функция
. Этому условию удовлетворяет функция ![]() , где
, где ![]() . Тогда
. Тогда ![]() будет стремиться к 0, если
будет стремиться к 0, если
![]() (3.15)
(3.15)
Рассмотрим, когда в нашем случае выполняется условие (3.15):
![]()
![]()
![]()
![]() (3.16)
(3.16)
Подставив известные параметры в уравнение (3.16), получим:
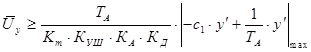 (3.17)
(3.17)
Теперь необходимо получить оценку параметра ![]() . Значение параметра
. Значение параметра ![]() получено путем обработки экспериментальных данных, представленных в [11]:
получено путем обработки экспериментальных данных, представленных в [11]:
![]() [
[![]()
].
Используя полученную оценку ![]() , подставим ее в (3.17):
, подставим ее в (3.17):
![]()
![]() =>
=> 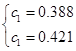 .
.
Таким образом, ![]() – область значений параметра
– область значений параметра ![]() , определяющего быстродействие системы, при котором выполняется неравенство (3.17), а значит, система будет асимптотически устойчива относительно поверхности скольжения и, следовательно, в ней будет возникать скользящий режим.
, определяющего быстродействие системы, при котором выполняется неравенство (3.17), а значит, система будет асимптотически устойчива относительно поверхности скольжения и, следовательно, в ней будет возникать скользящий режим.
Определение количества и объема складских емкостей
Для определения объема складских емкостей необходимо определить нормативный запас хранения (в сутках) вяжущего, в зависимости от его вида.
Расчет запаса цемента на складе. Табл.4.
Таблица.4.
Нормативный запас цементов
Вид цементов
ПЦ 300–Д0
ССПЦ 500 – Д20
ПЦБ 1 – 500 – Д20
сут.
8 ...
Мероприятия по охране труда и противопожарные мероприятия
При строительстве административного здания, перекладки и прокладки инженерных сетей, строительству и реконструкции инженерных сооружений, выполнению работ по благоустройству, озеленению и малым формам необходимо использовать современные средства техники безопасности и соблюдать правила охраны труда. Работаю ...
Экономическая оценка инвестиций
динамическим методом
Основными экономическими показателями эффективности инвестиций, учитывающими фактор времени, являются:
- чистый дисконтированный доход NPV – разность совокупного дохода от реализации продукции, рассчитанного за период реализации проекта и величины инвестиций:
где Р – годовые доходы руб.;
r – дисконтная ...
Категории сайта
- Главная
- Расчеты в строительных работах
- Современная технология терраццо
- Железобетонные конструкции и изделия
- Плавательный бассейн
- Ремонт оштукатуренных поверхностей
- Информация по архитектуре

