Расчет верхней части колонны

Подбор сечения верхней части колонны.

Расчетные усилия для верхней части колонны принимаем в сечении 2-2:

Продольная сила

N=471,93 кН,

Изгибающий момент

М=41,65 кН×м.

Сечение верхней части колонны принимаем в виде широкополочного двутавра высотой 0.5 м.

Для симметричного двутавра:

ix » 0.42×h=0.42×0.5=0.21 м;

rx » 0,35×h =0.35×0.5=0.175 м.

Условная гибкость:

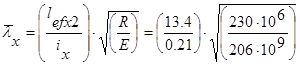=63.8×0.0334=2.13.

Относительный эксцентриситет приложения нагрузки:

mx=M/(N×rx)=41,65·103/(471,93·103·0.175)=5,04.

Примем в первом приближении:

Af/Aw=1.

Коэффициент влияния формы сечения по таблице 73 СНиП:

h=1.4-0.02× = 1.4-0,02·2.13=1.36.

Приведенный эксцентриситет:

mef=h×mx=1.36·5,04 =6,84.

Коэффициент для проверки устойчивости внецентренно-сжатых сплошностенных стержней в плоскости действия момента по таблице 74 СНиП: je=0.17.

Требуемая площадь сечения:

Aтр=N/(je×Ry)=471,93·103/(0.17·230·106) = 120,7 см2

По сортаменту подбираем двутавр широкополочный 50Ш4.

Геометрические характеристики сечения:

h=0.501 м,

bf=0.3 м,

tf=0.0235 м,

tw=0.0165 м,

A=0.02217 м2,

Jy=10599,999 см4,

Jx=96149,984 см4,

Wx=3838 см3,

iy=0.0692 м,

ix=0.2082 м.

Проверка устойчивости верхней части колонны в плоскости действия момента.

Площадь полки:

Af=bf·tf=0.3·0.0235=0.00705 м2,

Площадь стенки:

Aw=tw·hw=0.0165·(0.501-2×0.0235)=0.0075м2.

Af /Aw=0.00705/0.0075=0.94.

Условная гибкость:

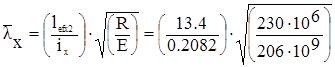=2.15

Относительный эксцентриситет приложения нагрузки:

mx=M×A/(N×W)=41,65·103×221,7·10-4 /(471,93·103·3838×10-6)=0,5.

Коэффициент влияния формы сечения:

h=(1.75-0.1×mx)-0.02×(5-mx)×= (1.75-0.1·0.5)-0.02·(5-0.5)·2.15=1.5.

Приведенный эксцентриситет:

mef=h×mx=1.5·0.5=0,75.

Коэффициент для проверки устойчивости внецентренно-сжатых сплошностенных стержней :

je=0.636.

s=N/(je×A)=471,93·103/(0.636·221.7·10-4)=33,4 МПа<Ry=230МПа.

Колонна устойчива в плоскости рамы.

Проверка устойчивости верхней части колонны из плоскости действия момента.

Гибкость верхней части колонны из плоскости действия момента:

ly= lefy2/iy=3.32/0.0692 =47,98.

Коэффициент продольного изгиба по таблице 72 СНиП:

jy=0.895.

Для определения mx найдем максимальный момент в средней трети расчетной длины стержня:

Mx1/3=41,65·2/3=27.76 кН×м,

по модулю Мх>Мmax/2=41,65/2=20.83 кН×м.

Тогда

mx=Mx1/3×A/(N×Wx)=27,76·103·221,7·10-4/(471,93·103·0.003838)=0,34 кН×м.

Так как mx<5 то коэффициент

с=b/(1+a×mх);

c – коэффициент учитывающий влияние момента на устойчивость внецентренно-сжатого стержня, из плоскости действия момента (учет изгибно-крутильной формы потери устойчивости).

Значения a и b определим по таблице 10 СНиП:

Коэффициент a=0.7

=47,98<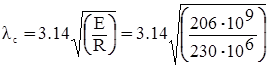=94.012,

следовательно b=1.0.

Тогда с=b/(1+a×mx)=1/(1+0.7·0.34)=0.8.

Проверку устойчивости колонны из плоскости действия момента проводим с учетом всей площади сечения, так как обеспечивается условие местной устойчивости стенки (прокатный двутавр).

s=N/(с×jy×A)=471,93·103/(0.8·0.895·221,7·10-4)=29.7МПа<Ry=230 МПа.

Колонна устойчива из плоскости рамы.

Синтез алгоритмов управления тепловым режимом на станции. Расчет регулятора САУ ВТЗ. Постановка задачи синтеза регулятора САУ ВТЗ
Целью функционирования синтезируемой системы управления является поддержание необходимого расхода воздуха в тоннеле метрополитена. Требования, предъявляемые к качеству переходных процессов в системе управления производительностью вентилятора воздушно-тепловой завесы (САУ ВТЗ): tп 10 с, s30%, D5% Математич ...

Устойчивость плоской формы деформирования обеспечена. Стойка.
Расчетное усилие N2-3 =5976 кг. Расчетная длина lcm =3м. Требуемая площадь тяжа. , где тр =0.8 – коэффициент условий работы для болтов, работающих на растяжение; Rp =2100 кг/см2 – расчетное сопротивление растяжению черных болтов из стали Ст. 3. По прил.12 [2] принимаем dт = 27мм. Fбр = 5.722 см2, Fнт ...

Охрана труда и техника безопасности в технологии производства железобетонных изделий
При бетонировании в зимних условиях рабочие чаще всего получают в стесненных условиях тепляков ожоги паром, нередки случаи электротравматизма и отравления хлористым кальцием. К бетонированию в зимних условиях допускают рабочих, получивших специальный инструктаж и обеспеченных необходимой спецодеждой и сред ...