Реализация закона управления. Расчет дифференцирующего фильтра

Страница 2

Передаточная функция линейной части будет иметь вид:

(3.25)

Заменим , получим:

(3.26)

Избавимся от комплексной переменной в знаменателе выражения (3.26), для этого обе части дроби домножим на комплексно – сопряженную величину:

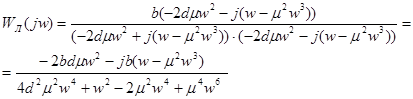(3.27)

Из выражения (3.27) выделим вещественную и мнимую части:

,

.

Приравниваем мнимую часть к нулю, откуда находим . Тогда линейная часть системы примет вид:

(3.28)

С учетом (3.21), (3.22) и (3.28), получим:

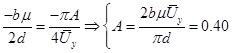(3.29)

Сопоставим полученные значения А и w с полученными значениями графоаналитическим способом в пакете Mathcad. На комплексной плоскости строим амплитудно-фазовую характеристику линейной части и АФХ нелинейного элемента (рис.3.22).

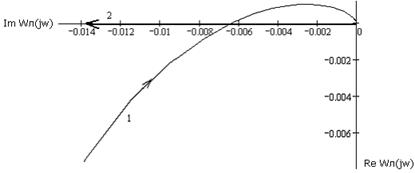
Рис.3.22. АФХ линейной части КБД (1) и обратная АФХ нелинейного элемента (2)

Точка пересечения АФХ Wл(jw) и АФХ 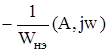имеет координаты (-0.0063,0), следовательно, по (3.13):

,

откуда

.

Частоту находим по АФХ линейной части, видя, что в точке пересечения характеристик Wл(jw) и 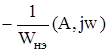мнимая часть Wл(jw)=0 воспользуемся соотношением:

(3.30)

Подставляя известные параметры в (3.30), определяем с-1.

Таким образом, найденные параметры автоколебаний соответствуют значениям, рассчитанным выше, т.е. устойчивым автоколебаниям.

Кадровое обеспечение
Необходимые трудовые ресурсы будут подбираться из жителей района и края. Край обладает развитой сетью профессионального образования. В нее входят 82 учебных заведений, из них 9 ВУЗов, 11 филиалов различных технических и гуманитарных институтов, 23 средних специальных заведений, 39 профессионально-технически ...

Определение степени агрессивного воздействия подземных вод и разработка рекомендаций по антикоррозионной защите подземных конструкций
Для железобетонных фундаментов на естественном основании серии 1.412–2/77, принятых на основе технико-экономического сравнения вариантов, и технологического приямка установим наличие и степень агрессивного воздействия подземных вод по данным химического анализа, для соответственных грунтовых условий. Для ф ...

Составление описи работ по текущему ремонту здания
Текущий ремонт жилых зданий заключается в систематическом и своевременном проведении работ по предупреждению преждевременного износа конструкций, отделки, инженерного оборудования и по устранению в них мелких повреждений и неисправностей. Текущий ремонт зданий разделяют на профилактический, проектируемый з ...