Формирование поверхности переключения

При синтезе системы со скользящим режимом математическую модель объекта управления необходимо представить в переменных состояниях (форме Коши). Имеем следующую систему:

,

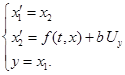где , .

Формируем желаемое дифференциальное уравнение на единицу меньшего порядка, чем уравнение объекта:

(3.11)

В статическом режиме y=V в силу свойств решения уравнения (3.11), где V – заданное входное воздействие на систему.

Параметр выбирается исходя из требований на время переходного процесса (3.10):

с-1. (3.12)

Желаемое характеристическое уравнение примет вид:

.

Теперь формируется поверхность переключения . Вектор состояния переменных имеет вид:

.

Тогда уравнение поверхности скольжения можно записать в виде:

(3.13)

Если обеспечить выполнение условия , то показатели качества будут определяться свойствами решений дифференциального уравнения (3.11).

Для организации движения вдоль заданного многообразия (поверхности скольжения) управляющее воздействие формируется в виде:

, (3.14)

где – размах реле, соответствующий ограниченному ресурсу управления объекта.

Определение планировочной отметки
По заданию, УГВ +1.000м., нулевая отметка земли 0.000м. Нормы осушения (глубины понижения грунтовых вод, считая от проектной отметки территории) при проектировании защиты от подтопления принимаются в зависимости от характера застройки защищаемой территории в соответствии с п.8.6 ,- на территории жилой застр ...

График потребности в основных строительных машинах и механизмах
При построении графика потребности в строительных машинах необходимо предусмотреть использование вспомогательных строительных машин и механизмов на отдельных работах, по которым в технологической модели не предусмотрены затраты машинного времени. При этом количество подъемников принимается из расчета по 1 м ...

Расчет свайного фундамента. Исходные данные
Свайные фундаменты возводятся в открытых котлованах. Их отличительными особенностями являются передача нагрузки на основание преимущественно через трение сваи об грунт и сопротивление под нижним концом сваи. Отношение высоты фундамента к ширине более четырех. Применение таких фундаментов обычно считается ра ...