Формирование и расчет неритмичных потоков с непрерывным использованием ресурсов

Страница 3

Общая продолжительность комплекса поточных работ определяется по формуле:

,

где сумма продолжительности работ в последнем частном потоке.

В заключение в соответствии с данными матрицы формирования строится сетевой календарный график производства поточных работ.

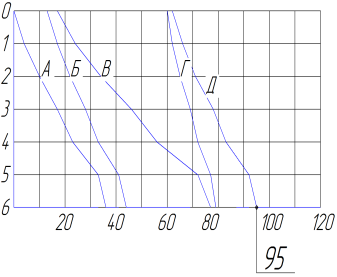
Рисунок 4 – Сетевой календарный график потока с непрерывным использованием ресурсов

Оптимизация потока по параметру времени производится за счет рациональной очередности освоения частных фронтов, позволяющей уменьшить суммарное значение периодов развертывания.

Расчет оптимизации производится по алгоритму Афанасьева-Джонсона. В основу расчета положено правило Джонсона (1954г), позволяющее выбирать рациональную очередность освоения частных фронтов для двухстолбцовой матрицы, описывающей взаимодействие двух частных потоков.

В исходной матрице поочередно рассматриваются все ее строки, и выявляется работа с наименьшей продолжительностью.

Если работа с минимальной продолжительностью расположена в первом столбце матрицы, то эта строка переносится на первое место и в дальнейшем не рассматривается. Если работа с минимальной продолжительностью расположена во втором столбце, то вся строка, содержащая эту работу, переносится на последнее место и также в дальнейшем не рассматривается. Зачем эта операция производится с оставшимися строками до полного перестроения исходной матрицы в оптимальную.

Профессором В.А. Афанасьевым (СПГУСиА) в развитие алгоритма Джонсона предложен алгоритм, позволяющий выбрать рациональную очередность освоения частных фронтов для неритмичного потока с непрерывным использованием ресурсов, состоящего из любого числа частных потоков. Алгоритм Афанасьева-Джонсона имеет следующую последовательность расчетов:

1. Исходная матрица из частных потоков разбивается на парных подматриц.

2. Каждая из парных подматриц оптимизируется по правилу Джонсона.

3. Каждая из оптимизированных подматриц поочередно принимается за генеральную, по которой переформировывается исходная матрица таким образом, что для всех ее столбцов принимается последовательность освоения, указанная в оптимизированной подматрице.

4. Для каждого варианта формирования рассчитываются периоды развертывания всех частных потоков. Минимальное значение суммы периодов развертывания будет соответствовать оптимальному варианту очередности освоения частных фронтов. В соответствии с оптимизированным вариантом матрицы формирования потока вновь строится сетевой календарный график производства поточных работ.

; ; ; .

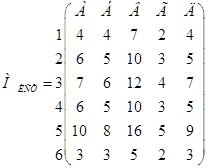
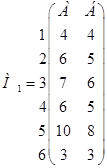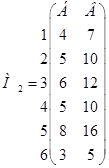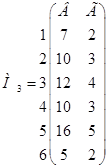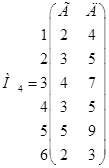Оптимизация по подматрице :

Определяем по правилу Джонсона оптимальную очередность освоения частных фронтов:

; ;

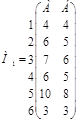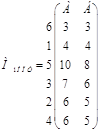В соответствии с методом Афанасьева принимаем эту подматрицу за генеральную, определяющую очередность работ, и вычисляем по ней периоды развертывания и общую продолжительность работ:

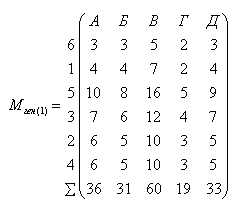
Табл. 24

Технико-экономические показатели
1. Объем работ: VB + Vрастит.слоя = 32681+22500=55181м3 2. Трудозатраты: 134,958 ч/смена 3. Выработка в натуральных показателях: 408,8 м3/ч.смена 4. Продолжительность работ по календарному графику: 20 дней. ...

Приходная часть теплового потока
Приходный поток, поступающий при сгорании топлива: где Х – удельный расход топлива, м3/с. Тепловой поток, поступающий с воздухом, нагретым в регенераторе: где Vα – расход воздуха для горения 1м3 топлива, м3; Св – удельная теплоемкость воздуха при температуре нагрева, кДж/(м3∙с); tв – т ...

Построение эпюр усилий в ригеле
Сначала вычисляем эпюрные моменты от четырех элементарных загружений 1. нагрузка g распределенная по всем трем пролетам; 2. нагрузка v, приложенная в первом и третьем, считая слева, пролетах рамы; 3. то же, во втором пролете; 4. то же в первом и втором пролетах. Для схемы 1 вычислим М12 Отношение пого ...